Matriz computacional
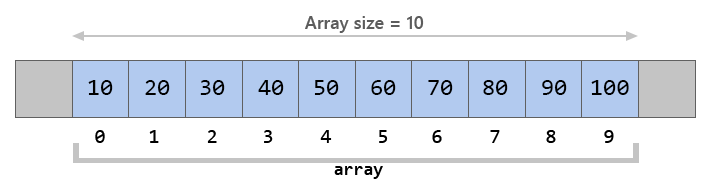
Uma matriz computacional é uma estrutura de dados bidimensional usada em computação para
representar conjuntos de números ou elementos organizados em linhas e colunas. É uma
estrutura fundamental em várias áreas da computação, como álgebra linear, processamento de
imagens, aprendizado de máquina e muitas outras.
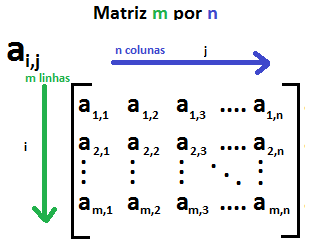
Em termos simples, você pode pensar em uma matriz como uma tabela de números. Cada elemento
da matriz é identificado por dois índices: um para a linha e outro para a coluna. Por
exemplo, uma matriz 3x3 teria três linhas e três colunas, totalizando nove elementos.
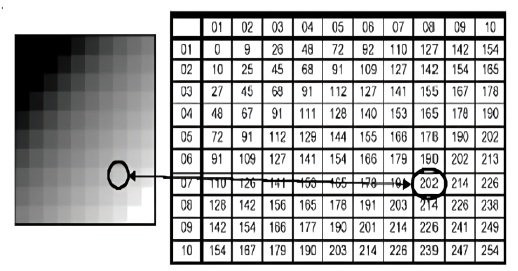
Matrizes computacionais são utilizadas para armazenar dados estruturados de forma tabular e
realizar uma variedade de operações matemáticas, como adição, subtração, multiplicação,
transposição, entre outras. Elas são essenciais em muitos algoritmos e cálculos que lidam
com grandes conjuntos de dados ou representam sistemas complexos.